论文地址：https://arxiv.org/pdf/1901.01928v1.pdf

一、背景

卷积神经网络已被证明在计算机视觉中传统的艰巨任务中是成功的，例如图像分类和目标检测。随着AlexNet的突破，ILSVRC中创建了许多新的拓扑来实现高精度。此类网络的成功不仅将注意力转移到如何做到这一点上，而且还转移到了它运行的速度和记忆效率上。这些模型以具有数百万个参数而闻名，即使使用GPU，它也需要更多的计算时间和比许多应用程序所需的更多的存储空间。

运行卷积神经网络时所需的大部分内存和计算工作都花在了卷积层中，例ResNet50超过90%的时间/内存。这意味着，为了让网络运行得更快更高效，我们必须提高卷积层的计算负载。

二、前言

考虑到这一点，研究者提出了一种新型的卷积层，我们称之为分布移位卷积（DSConv）。这种类型的层在设计时考虑了两个主要目标：（i）它应该大大提高标准卷积层的内存效率和速度；（ii）它应该是标准卷积的即插即用替代品，因此它可以直接用于任何卷积神经网络，包括推理和训练。

研究者通过将传统的卷积内核分解为两个组件来实现这一点。其中之一是只有整数值的张量，不可训练，并根据预训练网络中浮点 (FP) 权重的分布进行计算。另一个组件由两个分布移位器张量组成，它们将量化张量的权重定位在模拟原始预训练网络分布的范围内：其中一个移动每个内核的分布，另一个移动每个通道。这些权重可以重新训练，使网络能够适应新的任务和数据集。

三、新框架（DSConv layer）

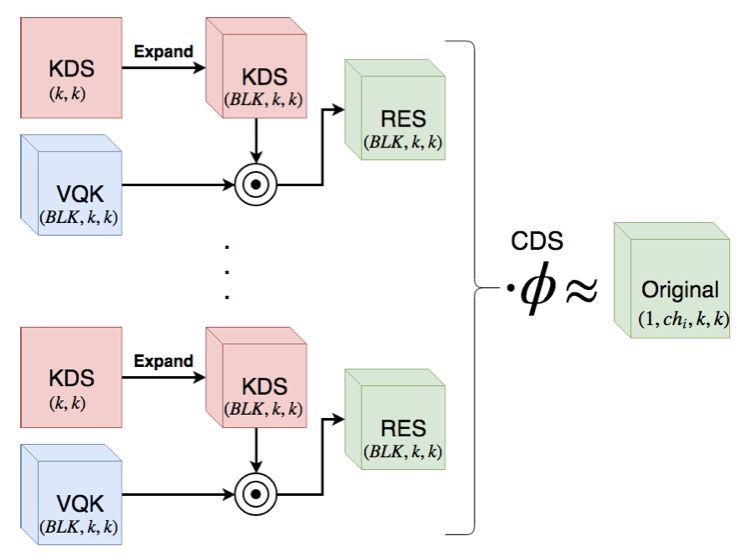
可变量化内核（VQK）：此张量仅保留可变位长整数值，并且与原始卷积张量具有相同大小的（ch0,chi,k,k），参数值被设置为从原始浮点模型量化，并且一旦设置不能改变，这是DSConv的量化组件。

分布移位：此组件的目的是移动VQK的分布以尝试模仿原始卷积内核的分布。通过使用两个张量转换两个域来实现。第一个张量是内核分布移位器（KDS），他改变每个（1，BLK,1,1）的分布。

例如，给定（128,128,3,3）的原始单精度张量大小，将位大小的超参数设置为2位且块大小设置为64，将保存2位整数的VQK的大小为（128,128,3,3）（量化后的，由单精度变整型），保持FP32编号的内核移位器（KDS）的大小为2*（128,2,3,3），保存Fp32编号的通道移位器的大小为2*（128），在此示例中，卷积内核减少到其原始大小的7%

使用此设置，VQK充当先验，它捕获特定切片应提取的特征类型的本质。

四、 Quantization Procedure

量化函数将要量化的网络的比特数作为输入，并将带符号的整数表示来存储。

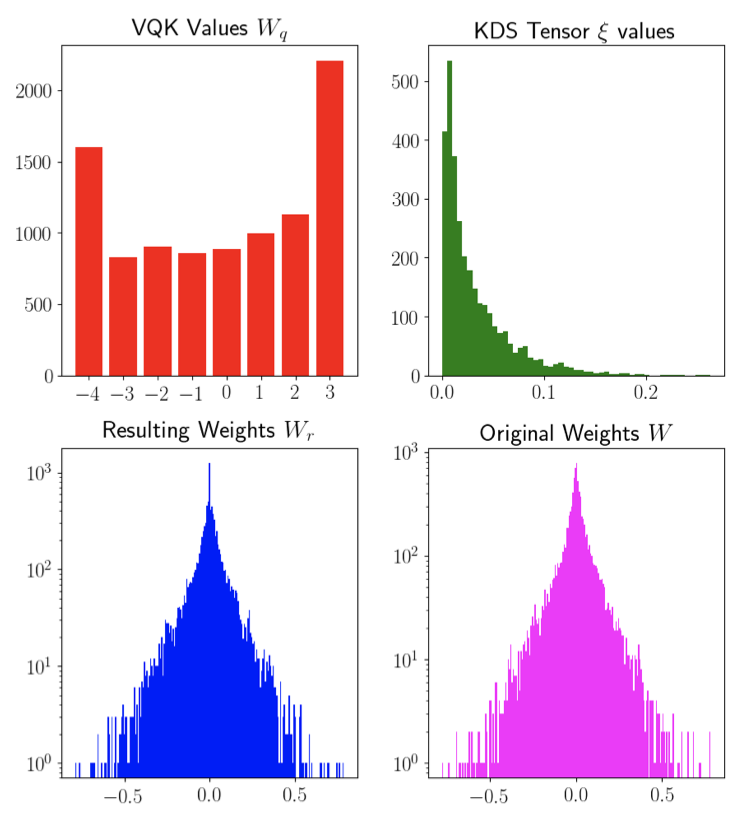
这是通过首先缩放每个卷积层的权重以使得原始权重w的最大绝对值与上面的量化约束的最大值匹配来实现的。再次步骤之后，将所有权重量化为最接近的整数，然后将新权重wq作为整数值存储到存储器中，以便稍后在训练和推理中使用。

五、 Distribution Shifts

分布转移的目的是移动VQK，使得输出和原始权重张量的值是相匹配的，这是通过内核中的分布偏移（KDS）以及通道中的分布偏移（CDS）来完成的，对其进行良好的初始化是有必要的，因为他会使网络最接近最佳值，只有在达到最大精度之前才进行微调。

KL-Divergence: 内核分布器移位后产生的VQK应该具有与原始权重类似的分布。量化过程仅适用缩放因子来评估VQK的整数值

最小化L2范数：初始化内核移位器张量的值，使得逐元素乘法后的结果尽可能接近原始值。

两种方法效果是一致的。

六、 Optimized Inference

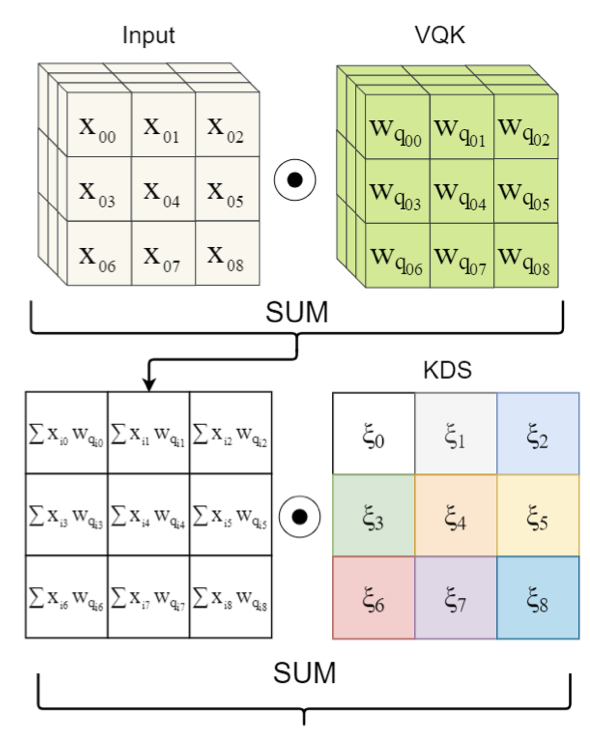
首先将它乘以输入张量，而不是移动VQK，这意味着大部分操作将以整数值而不是浮点数计算，根据所使用的硬件，这可以通过8位操作实现2-10倍的加速。使硬件可以利用整数运算而不必使用浮点运算。

给定BLK的块大小，当chi是BLK的倍数时，该方法将执行比其原始对应物少的FP乘法的BLK倍。对于块大小为128，通过简单的将卷积层更改为DSConv，将显著减少2个量级的fp乘法

在执行给定内核中所有卷积的总和之后，将在稍微应用信道分布移位，进一步改善存储器和计算能力，如果模型在卷积运算符之后包括它，则可以将通道移位合并到BN中。

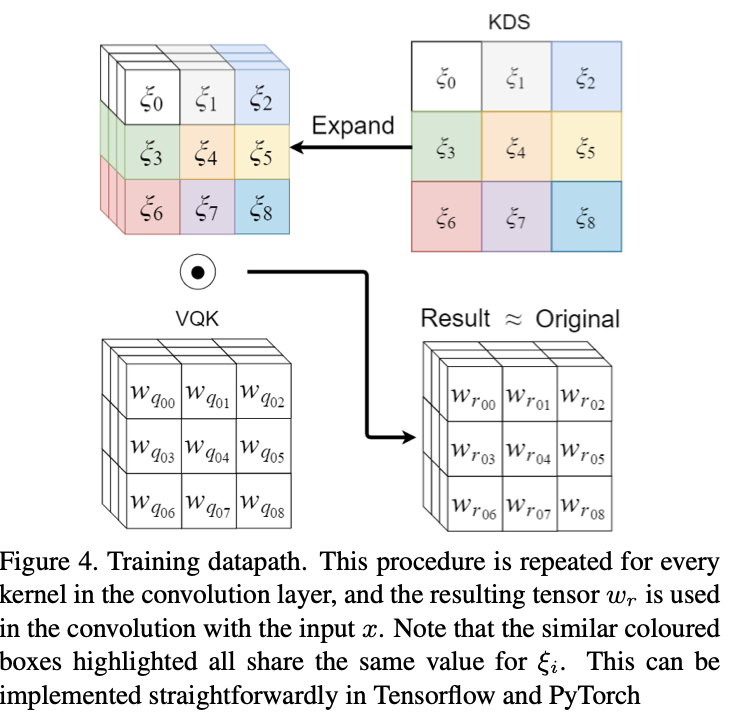
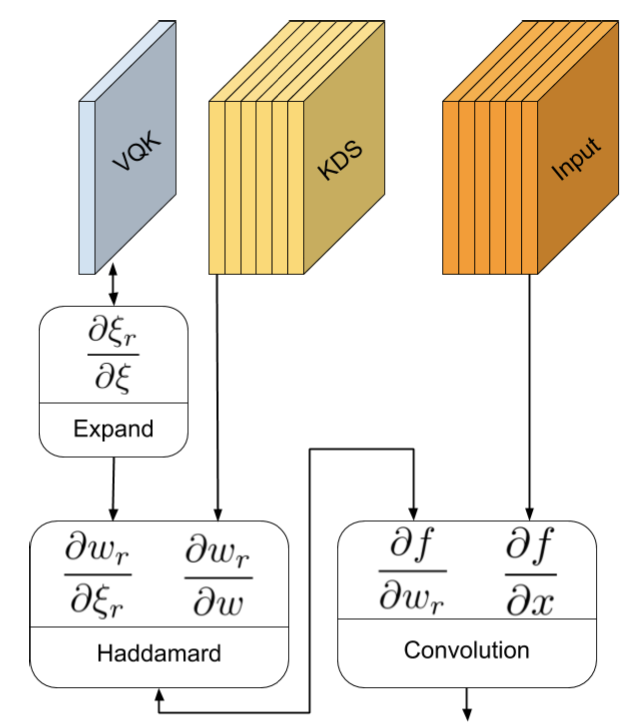
使用此过程，也可以很容易地计算方向传播。借助上图可以看出方向传播被简单地分解为三个简单的操作。还应该注意的是，VQK核是不可训练的，因此不需要计算∂wr/∂w的值。相反，只需要计算∂ξr/∂ξ，它的大小明显小于∂wr/∂w。

七、 实验

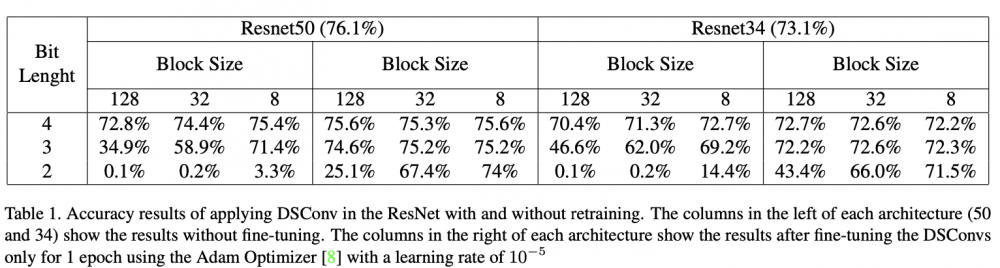
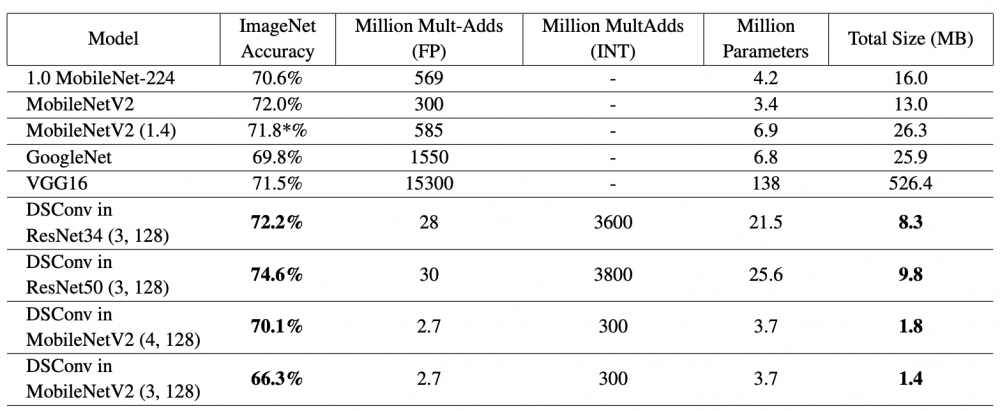
*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。