(文献阅读) LiTAMIN2: Ultra Light LiDAR-based SLAM using Geometric Approximation applied with KL-Divergence

论文作者：Masashi Yokozuka, Kenji Koide, Shuji Oishi, Atsuhiko Banno

文章来源：ICRA2021论文（点云配准）

视频、论文地址：在公众号「计算机视觉工坊」，后台回复「LiTAMIN2」，即可直接下载。

其中的版本1，LiTAMIN: LiDAR-based Tracking And Mapping by Stabilized ICP for Geometry Approximation with Normal Distributions.

可参考博客：https://blog.csdn.net/Yong_Qi2015/article/details/114528734；

论文链接：https://ieeexplore.ieee.org/document/9341341

翻译：chaochaoSEU

摘要：本文提出了一种可用于500-1000hz处理的3D LiDAR SLAM方法。该方法利用一种新的ICP度量，显著减少了点云配准的点数，同时保持了配置精度。当点数减少时，采用ICP法的点云配准就不那么准确了，因为ICP基于的是点之间的距离最小化。为了避免这一问题，将对称的KL-散度引入到反映两个概率分布之间差异的ICP代价函数中。代价函数不仅包括点之间的距离，还包括分布形状之间的差异。在KITTI数据集上的实验结果表明，该方法具有很高的计算效率，性能优于其他方法，并且与现有最先进的SLAM方法具有相似的精度。

1 引言

同时定位与建图（SLAM）是移动技术和服务的一个基本元素，如自主移动机器人。特别是，LiDAR和深度传感器已经被商业化，且由于其稳定和准确的性能而正在被应用。在不久的将来，不仅是自动驾驶的汽车，而且所有类型的移动设备都将配备激光雷达或深度传感器。我们预计，在这样一个世界中，通过SLAM获取的点云数据将被聚合到云端并共享以提供各种服务。

有必要从全球的设备中实时聚合的大量点云数据中有效地生成和更新世界地图。由于在此过程中使用的服务器的数量比设备的数量要小得多，因此必须使用超出实时性能的SLAM方法。目前LiDAR-SLAM的性能只稍微好于实时性能。

除了服务器之外，操作边缘设备也需要加速，而边缘设备在计算资源方面受到了严重的限制。目前LiDAR-SLAM是基于使用CPU和GPU的PC保证实时性，提高SLAM方法的计算效率以确保边缘设备的实时性。

虽然许多研究已经在SLAM基准 [1]和追求精度的方法[2]-[14]上进行，但很少有研究已经显著提高了目前的计算效率。在未来，要集中、高效地处理大量的机器人和设备，SLAM方法将更加追求高速。

本文的目的是建立一种与最先进方法一样准确的方法，同时实时性显著超过当前方法。本文讨论了一种3D LiDAR-SLAM，其显著提高了LiDAR-SLAM的计算效率，可在500-1000 Hz下运行，且提供了与最先进方法相同的精度。该方法在保持精度的同时，使用一种新的ICP度量，显著减少了用于点云配准的点数。采用ICP的点云配准方法在点云数较少时，精度低。为了避免这个问题，引入了对称的ICP代价函数。实验结果（图1)表明，该方法具有很高的计算效率，性能优于其他方法，并与最先进SLAM方法有相似的精度。

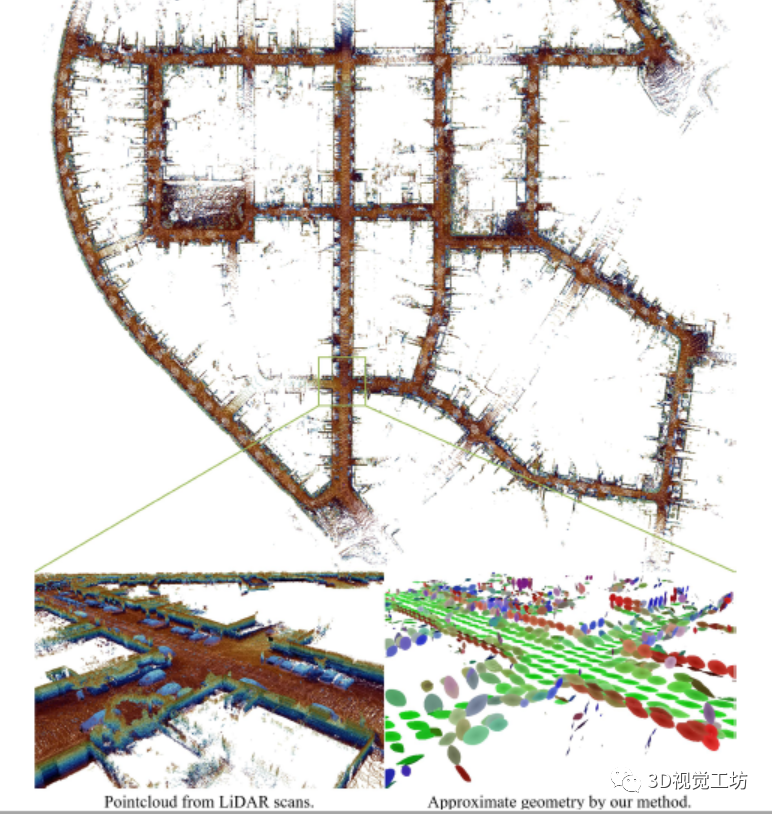
图1 使用LiTAMIN2的KITTI数据序列00的示例建图结果。右下角图的颜色表示由主成分分析分解的正态分布给出的正态方向，该方向是最小特征值的特征向量。

2 相关工作

LiDAR-SLAM方法可以分为两类：基于 ICP的方法[2]-[8]和基于特征的方法[9]-[14]。

对于基于ICP的方法而言，体素化是一种简单而有效的加速方法。通过将点云划分为小群，并以正态分布逼近每个子点云，可以在一定程度上在保持形状的同时显著减少点的数量。正态分布变换(NDT)[15]-[17]和GICP[18]是执行体素逼近的最常用的icp方法，但它们之间存在一些区别。NDT只逼近具有正态分布的目标点，并确定体素对应，而GICP对目标点云和源点云进行正态分布逼近，并使用KD树的精确最近邻搜索寻找相关性。NDT的计算效率往往更高，而GICP则往往更准确。

基于特征的方法是从LiDAR数据中提取点、线、面等几何特征，并有效地确定对应关系。LOAM[9]是第一个使用特征方法进行快速和准确的LiDAR里程计。它使用特征匹配显著减少了定位阶段所需的点数。LeGo-LAOM [11]只依靠良好的性能来执行特性选择，是目前可用的最快方法之一[2]。

为了实现更快的配准，一些方法利用GPU的计算能力，包括SuMa[4]、Elastic-Fusion [6]、Elastic-LiDAR Fusion [5]和Droeschel等的方法[8]。它们将LiDAR数据的形状近似为Surfel (面元)[19]。Surfel是一种基于点的渲染方法[20]，它旨在用点云而不是多边形网格来渲染三维形状，并且适用于GPU处理。因此，它允许通过使用硬件支持的投影数据关联来实现快速的点对平面ICP[21]的性能。

基于深度神经网络的LiDAR里程计[22]-[24]的方法也已经流行起来。LO-Net[22]是一种端到端的LiDAR里程计。虽然用于训练和测试的数据变化较少，但它显示的精度与传统方法相似。LO-Net主要是卷积张量运算，这使得点对点处理的并行化更加容易，对GPU的未来演化也可扩展。然而，端到端里程计估计是否可在未学习的环境和运动下工作尚未得到足够的研究，因此需要进一步的研究。

当前的LiDAR SLAM方法大约需要N点数的O（N）或O（Nlog（N）），并且从理论上讲，应该引入不同的方法来改进算法。本研究中的主张简单明了：基于ICP的方法所需的点数应该少。通常，基于ICP的方法的准确性会随着点数的减少而降低；因此，应该找到一种方法来解决速度和精度之间的权衡问题。

3 数学模型

在本节中，我们描述了该方法与LiTAMIN[2]之间的差异；这些差异是用于减少点数的方法和使用ICP代价函数。

A.减少点数

如图2所示，LiTAMIN将一组输入点投****到体素网格中，使用投****点的方法对齐它们，并将点云集成到体素图中。该方法以类似的方式执行SLAM，但不同之处在于，它对输入点组的投****结果使用了协方差，而不仅仅是平均值。而LiTAMIN是一种point-to-normal分布建图，该方法将其扩展到distribution-to-normal分布建图。这是为了通过考虑分布来提高准确性。该方法增加了每个体素的大小，减少了点数，这大大降低了计算成本。此外，它通过考虑分布的形状而不是点来避免了精度的损失。

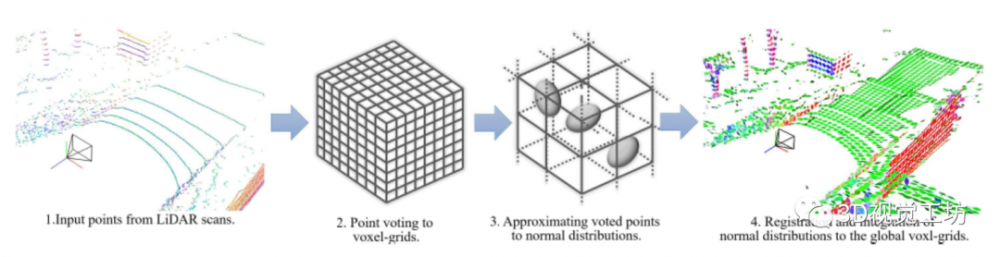
图2 我们的方法概述。右图的颜色表示通过使用主成分分析分解的正态分布给出的法线方向；颜色类似于图1中的颜色。

B．应用于对称KL散度的ICP代价函数

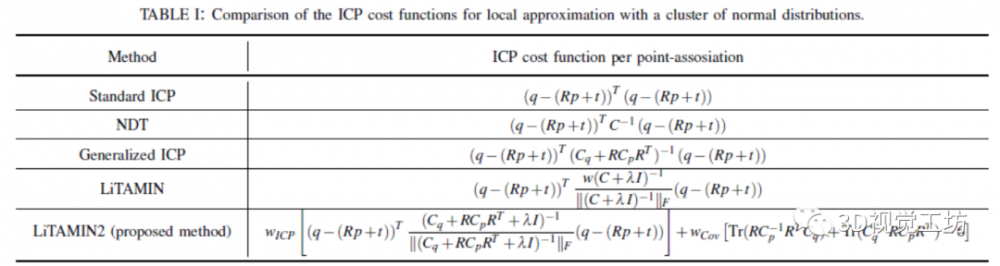
表1显示了现有方法和所提方法的ICP代价函数。该方法与其他方法的区别在于，代价不仅考虑了点之间的距离，还考虑了分布的形状。虽然其他的方法，如NDT[15]，GICP[18]和LiTAMIN [2]，已经考虑了协方差，但在实践中，它们只通过加权协方差的倒数来评估距离。该方法同时计算第一项的加权距离和第二项的分布形状差异。例如，如果点之间的距离很小，但分布的形状不匹配，则代价函数被设计为很大。这个代价来自于两个高斯分布p和q[25]的KL-散度DKL(p||q)[26]：

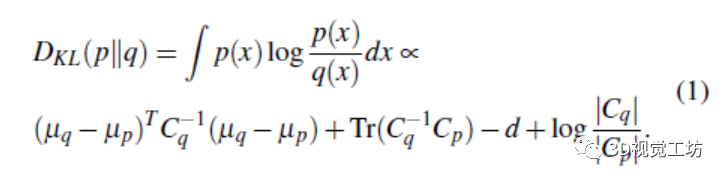
KL-散度是对分布之间差异的一种度量，它不仅代表了平均值之间的差异，而且还代表了分布形状之间的差异。KL-散度的目的是进行一个考虑到分布形状的鲁棒配准。

然而，KL-散度DKL(p||q) ≠DKL(q||p)并不对称：它通常被认为不是一个距离。由于ICP是一种距离最小化算法，需要更合适的度量，因此使用DSymKL(p||q)，本研究引入了以下对称性：

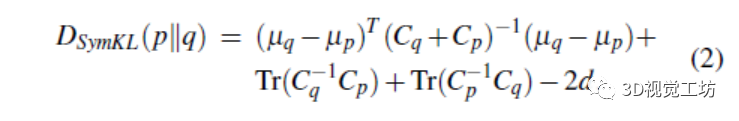
通过在DSymKL(p||q)中应用归一化，并引入刚体变换R和t，得到了代价函数，为了进一步解决异常值，ICP误差EICP和分布形状误差ECOV设置如下：

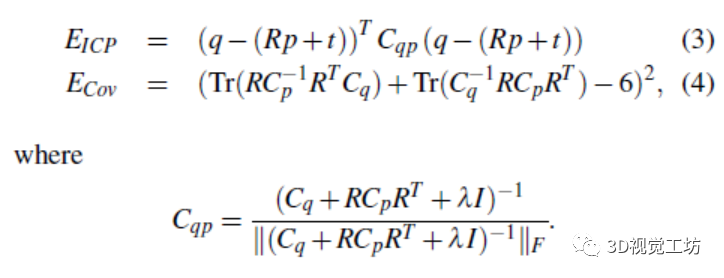
另外，其权重如下：

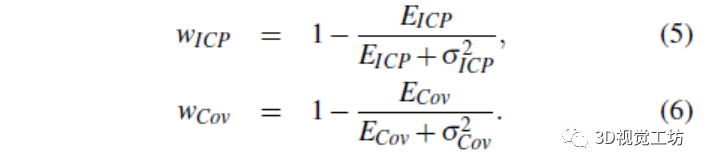
在表1中，考虑到LiTAMIN的两个分布的协方差，所提出的方法的第一项可以看作是ICP代价。与LiTAMIN主要区别是第二个代表分布形状差异的术语。在本研究中，引入这个项，使精度不会降低，即使点的数量因为大的体素大小而大大减少。它可以只计算第一项，即ICP代价。因此，研究了仅是第一项的情况与实验中第一项和第二项组合的情况之间的差异。

C.实现和参数

本研究利用牛顿方法优化了该方法的代价函数。由于代价函数的第二项不是平方误差，它需要先求Hessian，并且使用牛顿法，而不是高斯-牛顿方法。这项研究没有使用LM法[27]的阻尼因数，因为没有它的计算是稳定的。

σICP和σCov的可接受值分别根据经验设置为0.5和3。sigmaICP对应于到Cqp的Mahalanobis距离，这意味着低于0.5的对应点是可信任的。σCov对应于ECOV；如果Cq和RCpRT相同，则ECOV = Tr（I）+ Tr（I）-6应该为0。在DSymKL(p||q)中，-2d是使DSymKL的最小值为0的项。将σCov= 3设置为允许在没有该术语的情况下允许的大约一半的误差。如在LiTAMIN中一样，Frobenius归一化的参数lambda设置为10-6。

LiTAMIN使用权重w的占用概率[28]，而所提出的方法使用wICP和wCov代替。对于闭环检测，使用了建议的ICP代价。其他元素使用与LiTAMIN中相同的参数和实现。除LiTAMIN外，还使用KD树搜索了ICP的相应点。关于图的表示，除了LiTAMIN以外，还使用了体素图。体素贴图用于减少构成贴图的正态分布的数量。

4 实验分析

A．对比

几种最先进的方法被选择为使用不同加速算法的竞争对手，特别是LiTAMIN、 SuMa、 LeGO-LOAM、 LOAM、 hdl-graph-slam[3], LO-Net 和 DeepLO。在SuMa项目页面上提供了一个详细的评估，因此在研究中提到了这个问题，而计算时间是由运行开源的研究人员获得的。在接下来的实验中，我们还利用LeGO-LOAM、LOAM、hdl-graph-slam的开源来获得轨迹和测量计算速度。关于LO-Net，使用了原论文的结果。

B.评价基准和标准

实验中使用了KITTI视觉基准测试，它包含了Velodyne HDL-64E S2在多个环境中获取的点云。因此，它允许评估由任何SLAM方法获得的轨迹。所提供的点云已经被分解，因此它们被直接输入到所提出的方法和竞争对手中。

根据以下三个标准评估每种方法的性能：

1） KITTI stats。KITTI Vision Benchmark [1]统计数据，即KITTI统计数据，用于准确性评估。这些标准使得能够使用相对于地面真实情况的相对关系来评估估计轨迹的质量。在这项研究中，以这种方式针对不同的长度（特别是每100 m至800 m）计算了平移和旋转误差，并计算了误差的平均值。基准提供的代码用于计算KITTI统计信息。

2）Absolute Trajectory Error（ATE）：为了评估每种方法的闭环性能，还计算了ATE [29]。ATE是相对于地面真实情况的绝对位置和姿态误差的指示器。KITTI统计信息是子轨迹误差的平均值，可能会低估闭环的影响；但是，ATE允许基于绝对误差评估比较由闭环修改的轨迹的整个形状。

3）Total time and frame rate：作为计算效率的指标，计算了处理KITTI Vision Benchmark的所有序列（包括闭环）所花费的总时间。还介绍了里程计的帧频，以评估位置估计的速度，这对于某些实时应用可能很重要。

C. Ablation study

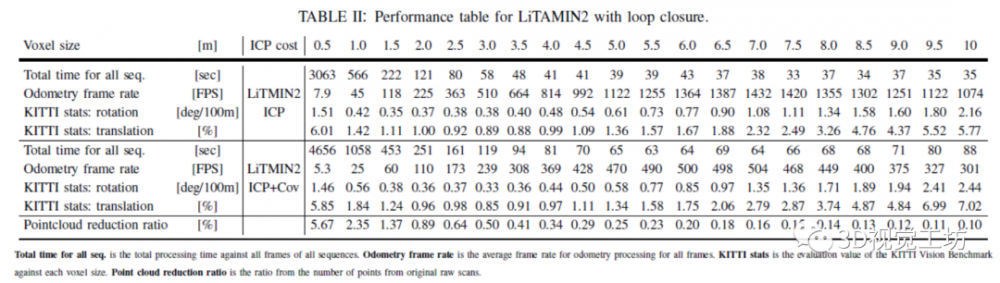
所提出的方法将在每个体素中投****的子点云近似为正态分布。由于体素大小会显着影响性能，因此针对不同体素大小对提议的方法进行了全面评估，如表2所示。此外，表2显示了使用体素化处理从原始扫描点开始的平均减少百分比。从KITTI统计数据来看，体素越精细，准确性就越不总是这种情况。请注意，在以下实验中，体素大小固定为3米，因为使用此值可获得最佳性能。

D.对比分析

表3显示了KITTI统计数据的比较。对于SuMa，比较了从作者的项目页面获得的轨迹数据集，帧到帧，帧到模型以及带循环闭合的帧到模型。对于LeGO-LOAM和hdl-graph-slam，实现了闭环，但是由于在我们的实验中未进行闭环检测，因此结果未在表3中列出。对于LOAM，考虑了在他们的论文中使用开源的测量结果以及原始论文的结果。原始序列中列出了各个序列的统计信息，但最终的KITTI统计数据未在表3中列出，因为它们未在原始论文中列出。LO-Net未在表3中列出，因为在[22]中提供了各个序列的统计信息，但未提供所有最终误差值的平均值。

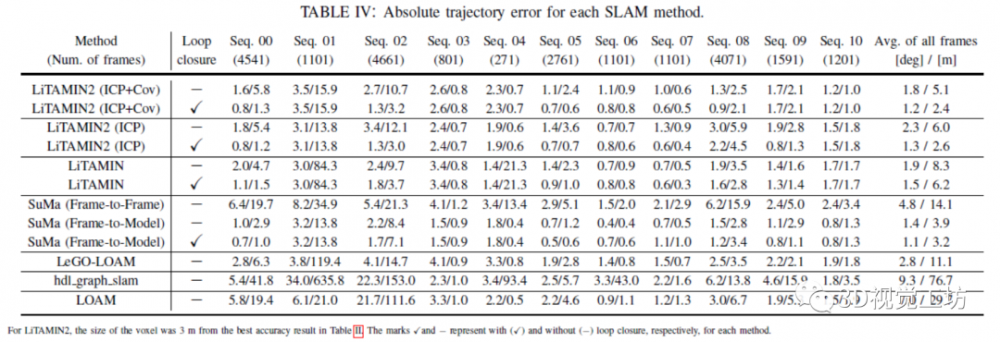
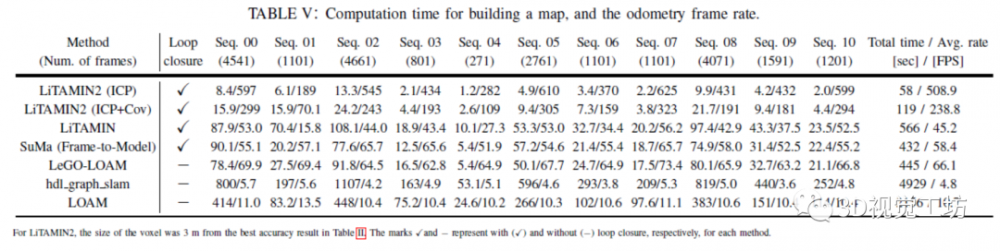
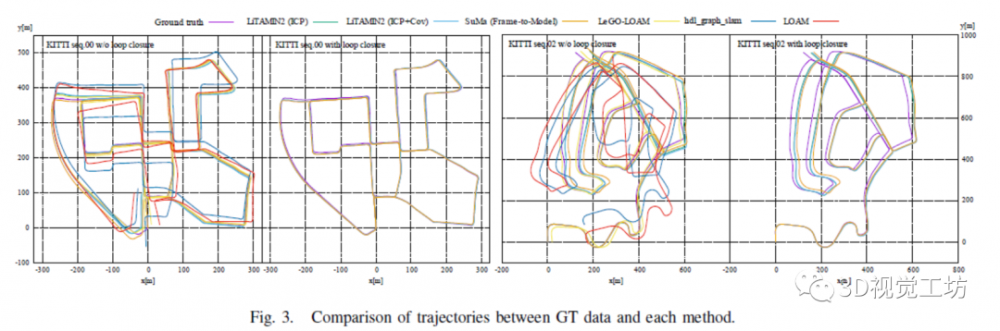
表4表示ATE的比较。除表2外，还对SuMa的结果进行了评估，分析了从作者的项目页面获取的轨迹。对于LOAM，将显示开源软件的结果。LO-Net被排除在表4中，因为ATE的结果未包含在原始论文中。表5显示了使用KITTI的每个序列和测距法过程的平均帧速率创建地图所花费的处理时间。所提出的方法LiTAMIN和SuMa显示了包括循环闭合在内的处理时间，因为这些方法中的循环闭合对所有序列都是成功的 SuMa结果是在本研究使用的计算机上使用开放源代码获得的，因为SuMa原始论文中的计算机规格不同。图3显示了每种方法的轨迹比较。左起的第二和第四幅图显示了所提出的方法和SuMa的闭环结果，但未显示其他无法检测到环路的方法。

总结

在这项研究中，提出了一种使用对称KL散度的ICP方法来显着提高LiDAR-SLAM的速度，并将其与其他最新的SLAM方法进行了比较。所提出的方法在里程计帧速率上实现了500 fps至1000 fps的计算速度，并且具有与其他方法相同的准确度，这证实了所提出的方法是从传统方法向前迈出的一大步。这是因为通过将点云从LiDAR投****到每个体素网格并将投****的子点云近似为一个正态分布，从而大大减少了用于配准的点数。尽管所提出的方法大大减少了点数，但是所提出的对称KL散度的ICP成本允许在不降低准确性的情况下处理数据。这些结果基于KITTI Vision Benchmark数据集，我们认为我们需要研究当使用环境发生变化时如何确定适当的体素大小。

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。