三维重建技术通过深度数据获取、预处理、点云配准与融合、生成表面等过程，把真实场景刻画成符合计算机逻辑表达的数学模型。这种模型可以对如文物保护、游戏开发、建筑设计、临床医学等研究起到辅助的作用。

一、研究背景及意义人类通过双眼来探索与发现世界。人类接收外部信息的方式中，有不到三成来自于听觉、触觉、嗅觉等感受器官，而超过七成、最丰富、最复杂的信息则通过视觉[1]进行感知的。计算机视觉便是一种探索给计算机装备眼睛（摄像头）与大脑（算法）的技术，以使计算机能够自主独立的控制行为、解决问题，同时感知、理解、分析外部环境。

20世纪60年代，计算机视觉得到了最初的发展。该阶段的研究重心主要体现在如何从二维图像中恢复出如立方体、圆柱体等立体化的三维形状，解释各个物体的空间位置关系。

1982年，David Marr[2]从信息处理的角度对数学、神经生理学、计算机图形学等学科的研究成果进行了归纳总结，并在此基础上提出了一系列计算机视觉理论。得益于这个完整明确的理论体系，计算机视觉得到了蓬勃的发展。它的核心思想是从二维图像恢复三维结构。图1-1展示的是经典Marr视觉信息处理过程。

图1-1 Marr视觉信息处理过程

随着科学技术的日新月异，计算机视觉的应用日益受到各行业的关注和重视，如设备检测与监视、医学图像处理、文物保护[3]、机器人视觉、自动导航、工业产品外观设计与生产等领域。计算机视觉技术为人们带来了机遇，也带来了挑战。

三维重建作为计算机视觉技术中最为最为热门的研究方向之一，涉及到包括图像处理、立体视觉、模式识别等多个学科体系。利用计算机建立表达现实客观景物的三维模型，并以此来满足生产和生活的需要。随着工业化进程的不断发展，多种技术的实现均有赖于目标物体三维信息的获取。三维重建现已被广泛的应用于生活和科研工作中，特别是在医学治疗、文物保护、游戏开发、工业设计、航天航海等方面，展现出了极强的生命力和影响力。

二、 三维重建技术简介

三维重建技术的重点在于如何获取目标场景或物体的深度信息。在景物深度信息已知的条件下，只需要经过点云数据[4]的配准及融合，即可实现景物的三维重建。基于三维重建模型的深层次应用研究也可以随即展开。人们按照被动式测量与主动式测量[5]对目标物体深度信息的获取方法进行了分类，下面对这两种方式进行相应的介绍。

1、被动式三维重建技术

被动式一般利用周围环境如自然光的反射，使用相机获取图像，然后通过特定算法计算得到物体的立体空间信息。主要有以下三种方法：

1.1 纹理恢复形状法

各种物体表面具有不同的纹理信息，这种信息由纹理元组成，根据纹理元可以确定表面方向，从而恢复出相应的三维表面。这种方法称为纹理恢复形状法[6] (Shape From Texture，SFT)。

纹理法的基本理论为：作为图像视野中不断重复的视觉基元，纹理元覆盖在各个位置和方向上。当某个布满纹理元的物体被投射在平面上时，其相应的纹理元也会发生弯折与变化。例如****收缩变形使与图像平面夹角越小的纹理元越长，投影变形会使离图像平面越近的纹理元越大。通过对图像的测量来获取变形，进而根据变形后的纹理元，逆向计算出深度数据。SFT对物体表面纹理信息的要求严苛，需要了解成像投影中纹理元的畸变信息，应用范围较窄，只适合纹理特性确定等某些特殊情形。所有在实际使用中较为少见。

1.2 阴影恢复形状法

SFS[7] (Shape From Shading，从阴影恢复形状)法也是一种较为常用的方法。考虑到图像的阴影边界包含了图像的轮廓特征信息，因此能够利用不同光照条件下的图像的明暗程度与阴影来计算物体表面的深度信息，并以反射光照模型进行三维重建。需要注意的是，像素点的亮度受到包括光源指标、摄像机参数、目标表面材质等的制约。

阴影恢复形状法的应用范围比较广泛，可以恢复除镜面外的各种物体的三维模型。缺点体现在过程多为数学计算、重建结果不够精细，另外不能忽视的是，SFS法需要准确的光源参数，包括位置与方向信息。这就导致其无法应用于诸如露天场景等具有复杂光线的情形中。

1.3 立体视觉法

立体视觉法[8]（Multi-View Stereo，MVS)是另外一种常用的三维重建方法。主要包括直接利用测距器获取程距信息、通过一幅图像推测三维信息和利用不同视点上的两幅或多幅图像恢复三维信息等三种方式。通过模拟人类视觉系统，基于视差原理获取图像对应点之间的位置偏差，恢复出三维信息。S.T.Barnard[9]等人对20世纪70年代到80年代之间出现的三维重建的算法和评价体系做了概述。

到了80年代中后期，出现了更多、更深层次的视觉原理，包括立体测量方法和深度传感器等，极大的促进了相关学科的发展。新兴方法可以直接获取景物的三维信息，极大的节省了物力与人力成本。U.R.Dhond[10]等人提出了基于层次处理的三目立体约束方法。二十世纪90年代末，涌现出诸如图像匹配的前沿算法、遮挡处理算法等。M.Z.Brown[11]等人总结了2000年到2010年间的三维视觉发展的总体概况，包括遮挡、配准和效率等的相关分析。

双目立体视觉重建，在实际应用情况优于其他基于视觉的三维重建方法，也逐渐出现在一部分商业化产品上; 不足的是运算量仍然偏大，而且在基线距离较大的情况下重建效果明显降低 。

代表文章：AKIMOIO T Automatic creation of 3D facial models 1993

CHEN C L Visual binocular vison systems to solid model reconstruction2007

作为计算机视觉的关键技术之一，立体视觉法也其弊端。例如，立体视觉需要假设空间的平面是正平面，而实际情况却与此相差甚远。除此之外，匹配还存在歧义性：对于一幅图像上的某些特征点，另外的图像可能存在若干个与之相似的特征点。那么如何选取最适配的匹配点，显得较为棘手。如图1-2所示，展示了Middlebury[16]数据集中Teddy和Cones场景的基准彩色图像、标准视差以及通过Graph Cuts[17]算法获取的立体匹配视差估计结果。虽然视差结果体现出了景物的三维位置关系，但是某些像素点的视差与标准值仍有细微的差距。除此之外，对于如相机运动参数的确定、大型场景重建需要获取多帧图像等问题，也极大的影响了立体视觉的深层次应用。

图1-2(a) 基准彩色图像

图1-2(b) 标准视差

参考：立体匹配导论

2、主动式三维重建技术

主动式是指利用如激光、声波、电磁波等光源或能量源****至目标物体，通过接收返回的光波来获取物体的深度信息。主动测距有莫尔条纹法、飞行时间法、结构光法和三角测距法等四种方法。

1.莫尔条纹法

莫尔条纹在生活中比较常见，如两层薄薄的丝绸重叠在一起，即可以看到不规则的莫尔(Morie)条纹；微风的吹动窗纱时，条纹亦随之运动。莫尔条纹法[18]起源于18世纪的法国，是一项古老又现代的测量方法。基本原理是将两块等间隔排列的直线簇或曲线簇图案重叠起来，以非常小的角度进行相对运动来形成莫尔条纹。如图1-3所示，在主光栅与指示光栅的交叉重合处，因光线的透射与遮挡而产生不同的明暗带，即莫尔条纹。莫尔条纹随着光栅的左右平移而发生垂直位移，此时产生的条纹相位信息体现了待测物体表面的深度信息，再通过逆向的解调函数，实现深度信息的恢复。这种方法具有精度高、实时性强的优点，但是其对光照较为敏感，抗干扰能力弱。

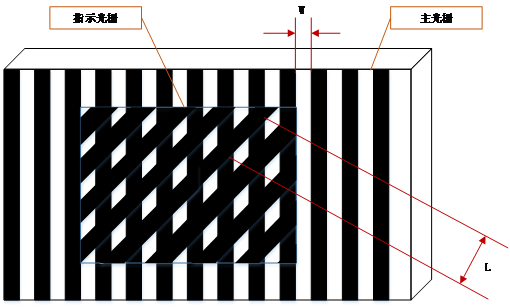
图1-3 双光栅莫尔条纹法

提出：WIKTIN recovering surface shape and orientation from texture (1987)（被引用454 次）。

发展：Warren 2010 对 wiktin 方法进行改进使用了****投影；

Liboy 2006 给出了在纹理单元结构发生改变的情况下的重建方法。

优点：精度高，对光照和噪声不敏感。

缺点：只应用于具有规则纹理的物体。

2.飞行时间法

飞行时间法[19] (Time of Flight，ToF)指的是在光速及声速一定的前提下，通过测量****信号与接收信号的飞行时间间隔来获得距离的方法。这种信号可以是超声波，也可以是红外线等。飞行时间法相较于立体视觉法而言，具有不受基线长度限制、与纹理无关、成像速度快等特点。但是其也有一定的缺点。首先，ToF相机的分辨率非常低。例如图1-4所示，当今分辨率最高的PMD Camcube 2.0 相机，也仅为204×204像素；其次，ToF相机容易受到环境因素的影响，如混合像素、外界光源等，导致景物深度不准确；最后，系统误差与随机误差对测量结果的影响很大，需要进行后期数据处理，主要体现在场景像素点的位置重合上。值得注意的是，ToF相机的售价达到了数万美元，受众较窄。

图1-4 SR4000 ToF相机

3.结构光法

结构光法[20](Structured Light)通过向表面光滑无特征的物体****具有特征点的光线，依据光源中的立体信息辅助提取物体的深度信息。具体的过程包括两个步骤，首先利用激光投影仪向目标物体投射可编码的光束，生成特征点；然后根据投射模式与投射光的几何图案，通过三角测量原理计算摄像机光心与特征点之间的距离，由此便可获取生成特征点的深度信息，实现模型重建。这种可编码的光束就是结构光，包括各种特定样式的点、线、面等图案。结构光法解决了物体表面平坦、纹理单一、灰度变化缓慢等问题。因为实现简单且精度较高，所以结构光法的应用非常广泛，目前已有多家公司生产了以结构光技术为基础的硬件设备，如PrimeSense公司的Prime Sensor、微软公司的Kinect和华硕公司的Xtion PRO LIVE等产品[21]。图1-5展示了利用结构光技术采集文物三维信息的场景。

提出：Woodham 对 SFS 进行改进（1980 年）：photometric method for determining surface orientation from multiple images (该文章被引用了 891 次)

发展：Noakes ：非线性与噪声减除 2003 年；

Horocitz ：梯度场合控制点 2004 年；

Tang ：可信度传递与马尔科夫随机场 2005 年；

Basri ：光源条件未知情况下的三维重建 2007 年；

Sun ：非朗伯特 2007 年；

Hernandez ：彩色光线进行重建方法 2007 年；

Shi ：自标定的光度立体视觉法 2010 年。

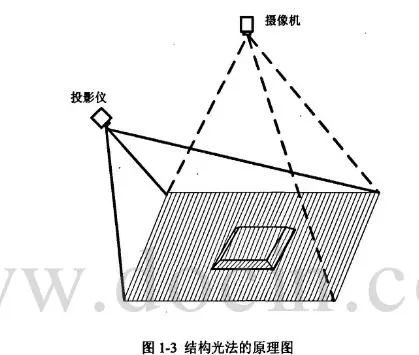
图1-5 结构光法原理图

4.三角测距法

三角测距法[22]是一种非接触式的测距方法，以三角测量原理为基础。红外设备以一定的角度向物体投射红外线，光遇到物体后发生反射并被CCD（Charge-coupled Device，电荷耦合元件）图像传感器所检测。随着目标物体的移动，此时获取的反射光线也会产生相应的偏移值。根据****角度、偏移距离、中心矩值和位置关系，便能计算出****到物体之间的距离。三角测距法在军工测量、地形勘探等领域中应用广泛。

参考文献

[1] Szeliski R. Computer vision: algorithms and applications[M]. Berlin: Springer, 2010.

[2] D. Marr, et al. A Computational Theory of Human Stereo Vision. Proc.R.Soc.Lond. 1979, B.204:301-328.

[3] Levoy, M. Pulli, et al. The Digital Michelangelo Project:3D Scanning of Large Statues. Proc.SIGGRAPH,2000.

[4] Anand A, Koppula H S, Joachims T, et al. Contextually guided semantic labeling and search for three-dimensional point clouds[J]. The International Journal of Robotics Research, 2013, 32(1):19-34.

[5] Mada S K, Smith M L, Smith L N, et al. Overview of passive and active vision techniques for hand-held 3D data acquisition [C]//Opto Ireland. International Society for Optics and Photonics, 2003: 16-27.

[6] D. A. Forsyth, J. Ponce, Computer Vision: A Modern Approach. Prentice Hall 2001

[7] Horn B. K. P. Shape from shading: a method for obtaining the shape of a smooth opaque object from one view. PhD thesis, Department of Electrical Engineering, MIT, Cambridge. 1970.

[8] Ikeuchi K. Determining surface orientations of specular surfaces by using the photometric stereo method [J]. Pattern Analysis and Machine Intelligence, IEEE Transactions, 1981, (6): 661-669.

[9] S. T. Barnard, M. A. Fisehler. Computational Stereo[J].ACM Computing Surveys. 1982, Vol.14:553-572.

[10] U. R. Dhond, J. K. Aggarval. Struct from Stereo—A Review [J]. IEEE Trans. Systems, Man, and Cybemeties.1989, Vol.19: 1489-1510.

来源：http://blog.csdn.net/wangyaninglm/article/details/51558310

作者：shiter@CSDN

编辑：3D视觉开发者社区

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。