对于新手来说，使用格雷码做单目结构光三维重建是一个入门级的训练。但是在复现时往往会遇到一个问题，明明解码都很不错了，重建后的点云精度却很低，甚至重建出来的平面点云出现断层现象。这是由于格雷码是一种离散型编码，编码精度是整数级的像素，这种编码设计注定了它的精度不会太高。所以在实际应用中，格雷码通常是配合着其他编码方式一起使用：比如使用格雷码来标示相移的周期数。

尽管如此，由于格雷码本身的特性，稳定性高，抗反光效果比较好，在精度需求不是特别高的情况下，还是有适用场景的。尤其是景深范围大的时候，相位很容易出现模糊，可是对于黑白条纹的格雷码适应的景深就能够大一些。本文就简单介绍下如何使用纯格雷码进行三维重建，并得到一个精度尚可的点云（至少不出现重建平面时明显断层/分层现象）。

从解决问题的本身出发，想要得到一个精度比较不错的点云，最直观的思路是解码时得到一个准确的亚像素级精度，比如像相移那样，但是对于格雷码而言，很难去给出一个很好的插值函数去获得一个亚像素级的匹配，实际上，如果以图片某一行为例，你得到的解码结果可能是 16,16,17,17,18，18,18，NaN，NaN，21… 对于这样排列的解码结果，想要用一个函数去定义亚像素的插值函数是一件很困难的事情，笔者暂时没有看到哪篇文章提供了好的思路。(如果有读者知道，欢迎和笔者沟通)。

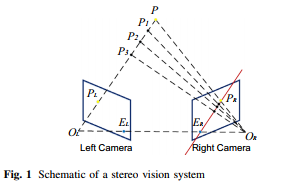
在无法获得准确的亚像素级的解码精度后，我们可以从三维重建方式本身去考虑,如上图所示。图中是一幅经典的双目重建模型，在之前的系列篇中我们介绍了单目结构光重建可以使用双目模型，只需要把投影仪看成一个逆相机就可以。图中红线即极线，也就是说，理论上相机成像点PL（图中left camera） 对应的可能的投影仪（图中Right Camra）中的位置是图中红线，如果知道对应的是图中红线哪一点，就可以解得准确的三维位置。

实际上，由于我们能够解得的编码只能是整数级的，导致我们的解码结果会像如下图所示的函数图一样，橙色的线是理论的极线，但是由于解码的离散性，我们得到的解码坐标是个整数级的数，如图中的阶跃函数，于是误差就这么产生了。

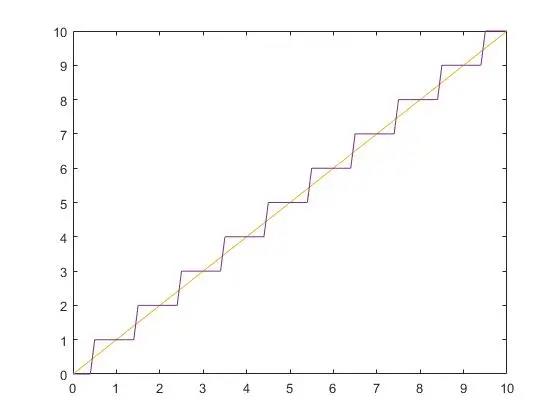
我们解得的点，通常会对应极线的或上方一点或下方一点，导致该点与投影仪中心点连线与相机像点和相机中心点发出的射线在三维空间不相交。如果相交，交点就是物体的在空间中的实际三维位置。尽管由于解码的离散性导致两条直线不相交，但是两条这空间直线间的距离不会很远，所以可以用如下思路去估计实际的物体三维位置：

求这两条空间直线中距离最近的两个点，而这两个点的中点就是我们估计的物体三维位置点。

这两个点怎么求呢？

在数学上很简单，我们高中都学过如何求三维空间中两条直线的距离，那条和两条直线都垂直且相交的线与两条直线的交点就是我们要求得的两条直线在空间中距离最近的两个点了！

至此，我们就很好的估计了一个比直接用解码结果按公式求得的更准确的三维重建点了，但是细心的朋友一定发现了，在一般形式的结构光三维重建中，我们仅仅需要用到列方向的条纹，（为什么仅需要一个列方向，可以看系列篇之三维重建原理），但是在上述求射线的过程中，我们需要知道像点对应的投影仪位置的行和列两个信息，如果仅有一个列方向的值，列所在的直线和原点就构成一个面了！那像点和相机中心连线的射线一定会和这个面有交点，且这个交点即是我们用传统的解法得到的解，这个解通常由于列值（格雷码）解码值精度不够而不够精确。

纯格雷码的三维重建并不算很常见，如果一定要用，不防试下上述方法，可以保证一定精度，当然还是没有相移法来的准确。还有一个显然的缺点就是投影的图片较多，需要行列方向都投影格雷码，投影图片数量太多会损失时间的效率，但是作为一个新手入门demo，还是很不错的选择！

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。