Harris 角点检测 认为 特征点具有局部差异性。

如何描述“特征点具有局部差异性”：

以每一个点为中心，取一个窗口，窗口大小为5*5或7*7像素大小。

这个窗口描述了这个特征点周围的环境。

如果这个特征点具有局部差异性，那么以这个特征点为中心，把窗口向360度任意一个方向移动，窗口的变化比较大，则这个特征点的周围环境变化比较大。

数学公式：

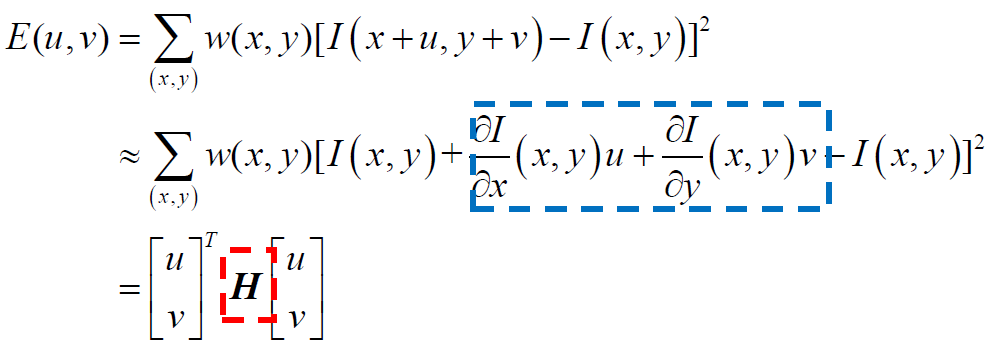
（x,y）：表示像素的位置。

：表示窗口内的每个像素。

w(x,y)：表示 这个位置的权重。

若w=1，则说明窗口中所有的像素贡献是一样的。

若w设置为以这个特征点为中心的高斯，

高斯权重，说明距离这个特征点越近，权重越大；越往周围发散，权重越小。

I(x,y)：表示(x,y)这个位置的像素值。如果是灰度图，I就是灰度值，如果是彩色图，I就是RGB值。

u和v表示窗口移动的方向。

I(x+u,y+v) - I(x,y)：表示对应像素的灰度差异。

：在整个窗口内，即在局部环境内求这个像素灰度差异的加权和。

对 I(x+u,y+v) - I(x,y)进行一阶泰勒展开，得到

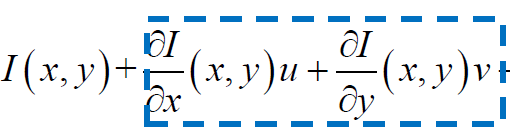
在(x,y)处的灰度值，再加上u方向和v方向的偏导数。

整理后，结果为：

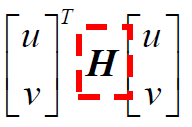
u和v表示窗口移动的方向， H表示Harris矩阵，主要由图像梯度表示。

对Harris矩阵进行特征分解：

得到两个特征值，矩阵的这两个特征值反映了：两个相互垂直的方向上的变化情况。

一个是变化最快的方向，一个是变化最慢的方向。

前面设置了u和v，这是两个向量，表示窗口移动的方向。以(x,y)这个点为中心，进行360度的旋转。

特征值对应的特征向量，确定了变化最快的方向和变化最慢的方向。其他方向的变化情况，介于这两者之间。

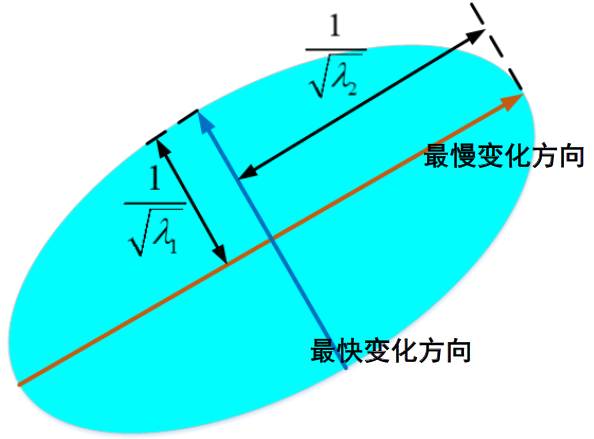
通过对Harris矩阵的分析，得到如下结论：

只有当Harris矩阵的两个特征值都非常大的时候，特征点才能和周围环境区别比较大，是我们想要的特征点。

现在检测特征的任务就变成了，计算Harris矩阵，并判断其两个特征值的大小。

Harris角点准则

实际中，并不对Harris矩阵进行分解求其特征值，因为计算量太大。而是使用Harris角点准则。

C = Harris矩阵的行列式值 – k(Harris矩阵的迹)2

Harris矩阵的行列式值：Harris矩阵特征值的乘积

Harris矩阵的迹：Harris矩阵特征值的和

·  k的值越小，检测子越敏感。k的值越小，能检测到的特征点越多。

·  只有当和同时取得最大值时， 才能取得较大值。

·  避免了特征值分解，提高检测计算效率。

本文仅做学术分享，如有侵权，请联系删文。

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。